j перпендикулярен как вектору k,
Решение
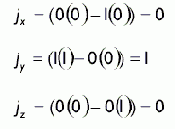
Таким образом, j = (0, 1, 0). Вспомните, в предыдущем разделе «Скалярное произведение векторов» говорилось, что если u Ч v = 0, значит u ^ v. Поскольку j Ч k = 0 и j Ч i = 0, мы знаем что вектор j перпендикулярен как вектору k, так и вектору i.
br>
Для вычисления векторного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
D3DXVECTOR3 *D3DXVec3Cross( D3DXVECTOR3* pOut, // Результат CONST D3DXVECTOR3* pV1, // Левый операнд CONST D3DXVECTOR3* pV2 // Правый операнд );
Как явствует из Рисунок 7, вектор –p также взаимно перпендикулярен векторам u и v. Какой из векторов, p или –p будет возвращен в качестве результата векторного произведения определяется порядком операндов. Другими словами, u × v = –(v × u). Это заначит, что операция векторного произведения не является коммутативной. Определить, какой вектор будет возвращен в качестве результата, можно с помощью правила левой руки. (Мы используем правило левой руки, поскольку работаем с левосторонней системой координат. Если бы у нас была правосторонняя система координат, пришлось бы воспользоваться правилом правой руки.) Если расположить пальцы левой руки вдоль первого вектора, а ладонь руки — вдоль второго, отогнутый на 90 градусов большой палец укажет направление результирующего вектора.
1 Теорема косинусов определяет зависимость между сторонами и углами треугольника. Она утверждает, что во всяком треугольнике квадрат длины стороны равен сумме квадратов двух других сторон без удвоенного произведения длин этих сторон на косинус угла между ними. Если угол прямой, то теорема косинусов переходит в теорему Пифагора, т.к. косинус прямого угла равен 0.